This post is about mindset, culture, implicit assumptions. The big assumption in neoclassical economics is ergodicity, or equilibrium, or stationarity, or stability — basically the idea that nothing ever changes fundamentally. Things may fluctuate but they always return to some state of normality. Naively, that doesn’t fit with the idea of a growing economy, innovation, and change. So something’s up. I’ll explore what that is by replacing the mental image of stability with something that doesn’t return to normality: a nuclear explosion.
E pluribus unum — micro to macro

Equilibrium thinking in economics has clearly traceable historical roots. Chapter 1 of Eric Beinhocker’s book is a wonderful summary of where it comes from. In short: it comes from equilibrium thermodynamics — the study of gases, liquids, solids, under conditions where everything is allowed to come to rest. This field developed in the 19th century when people were interested in steam engines. In other words, it was all about gases in boxes (steam in cylinders).
Social researchers of the 19th century were impressed by the success of this branch of science, and also by its similarity to economics. A gas is a macroscopic thing, characterized by macroscopic properties — temperature, pressure, volume. But it consists of many microscopic constituents (molecules) whose interactions collectively create the macroscopic state. The study of macroscopic properties arising from microscopic interactions is called statistical mechanics. That really does sound like economics: an economy is a macroscopic thing, characterized by macroscopic properties such as GDP and trade balances, and those macroscopic properties arise from myriad microscopic constituents (people) interacting with each other.
So far so good. I completely agree with the analogy at this level: economics really is about a lot of microscopic constituents generating macroscopic behavior. But… what was done in 19th-century thermodynamics and statistical mechanics was based on the assumption that things are well described as being in equilibrium. That is not the case in economics (we have growth), and a lot of equilibrium intuition simply doesn’t apply. More precisely, if there are quantities in economics that are sensibly described as being in equilibrium, then they will have to be carefully constructed — they’re secondary properties of the process, not the process itself.
Time and a non-field
This doesn’t invalidate the analogy between statistical mechanics and economics, it just says that we have to look at non-equilibrium statistical mechanics to learn from the analogy. So what do we have there? Non-equilibrium statistical mechanics is a much more varied field (this is always true for “non”-fields — by definition, they are anything but something specific). Also, the usual caveats apply: we’re doing science, not magic, which means we’re building a model that will capture some aspects of reality and give meaningful answers in a limited range of situations. Outside that range it will be invalid.
The big difference between equilibrium and non-equilibrium is the role played by time. In equilibrium, everything is allowed to come to rest, that means time is allowed to play out till the end before the system is studied. We set things up, then (mathematically) wait an infinitely long time, and then look where we’ve got to. Non-equilibrium statistical mechanics doesn’t do that. It doesn’t just look at the end state but at the transition to that end state — even more radical: it doesn’t assume that an end-state exists. In other words, it studies dynamics, it studies what happens as time passes (not where we get to at the end of time). Of course there are far more ways to get from A to B than there are As and Bs. The study of dynamics is more varied than the study of the end points of dynamics.

Capitalism
Now — what about that nuclear explosion? It’s a process that is not in equilibrium at all, and it was very important in the 20th century. In such an explosion, atomic nuclei break up. In doing so they release neutrons, and those neutrons can cause other nuclei to break up and release more neutrons that cause other nuclei to break up etc. — the famous nuclear chain reaction.
One important question is how many additional neutrons are set free due to the setting free of one neutron (averaged over all neutrons of one generation). If the number is greater than one, then we have a super-critical run-away solution. Something is producing more of itself. The process is fundamentally noisy, and it’s fundamentally multiplicative. The number of neutrons follows noisy exponential growth.
What else can generate more of itself? Capital. The genius of capitalism is to allow excess resources to be used to create more of themselves. Sometimes that works, sometimes it fails — the process is both noisy and multiplicative.
Let’s look at some data, and plot annual global GDP. For comparison, let’s plot its average (time-averaged over the plotted period) — if GDP was an equilibrium process it should hover around that value. For a nuclear explosion we could plot the number of free neutrons as a function of time. I don’t have data for this (direct measurement is a bit tricky, and detailed models are fairly confidential), but for a few hundred nanoseconds it will be exponential growth, so I’ll just plot exponential growth.
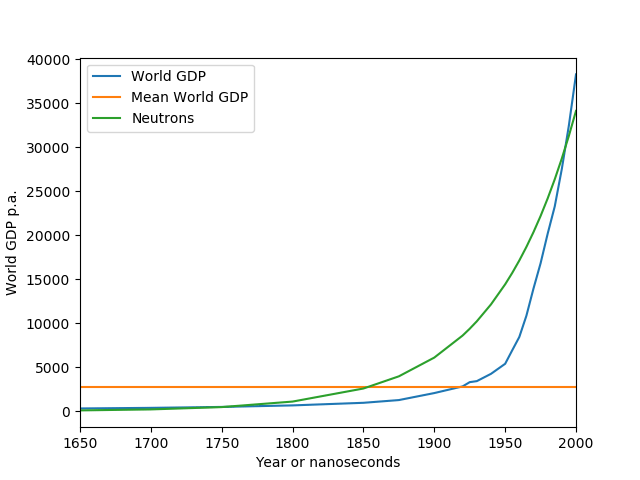
There are some differences between world GDP and exponential growth, but we’re definitely dealing with something that’s closer to a nuclear explosion (green line) than to an equilibrium process (yellow line). Of course the time scales are different, but economic growth and a nuclear explosion are similar.
When we model an explosion, we’re modeling a non-equilibrium process. Everything is flying apart, and naively there’s nothing stable about it. But there’s regularity even as things do fly apart — for example, for some limited time (while the chain reaction is running) each neutron sets free a more or less stable (certainly random!) number of new neutrons. We have to dig into the mechanics of the system to find something stable. Not impossible, but not trivial either.
Every economist knows that multiplicative growth is the null model not only for the nuclear explosion but also for the economy (GDP, asset prices etc). Nevertheless, the neoclassical economics mindset is one of equilibrium. That’s because some secondary properties of economic growth are quite stable (e.g. the exponential GDP growth rate), but equilibrium should not be our mindset. When we think about economics we should have the image of a slow nuclear explosion in mind. That’s very very different from the image of a gas in a box in equilibrium. The current formalism thinks: gas in a box in equilibrium. We think: explosion. Consequently, we will ask different questions and come to different conclusions about what we’re doing on planet Earth.
